leetcode14. Longest Common Prefix
by EunHye Jung
14. Longest Common Prefix
문자열 배열에서 가장 긴 공통의 접두사를 찾는 함수 작성.
만약에 공통적인 접수사가 없으면 공백(““)리턴 할것.
Example 1
Input: [“flower”,”flow”,”flight”]
Output: “fl”
Example 2
Input: [“dog”,”racecar”,”car”]
Output: “”
Explanation: There is no common prefix among the input strings.
Note
모든 입력된 문자들은 영소문자(a-z)임.
Leetcode Artcle
접근법 #1. Horizontal Scanning
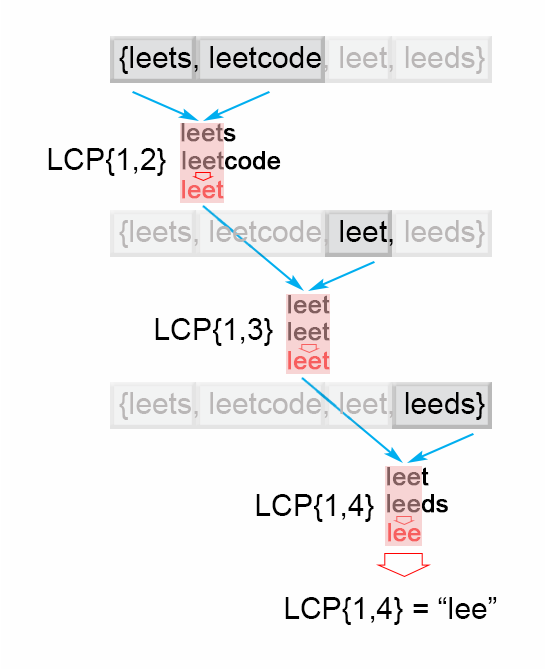
S1, S2, .. Sn까지의 문자열들이 주어질때, 가장 긴 접두사를 찾는 간단한 방법은 S1, S2에서 가장 긴 공통의 접사를 찾고, 그 결과값과 S3에서 가장 긴 공통의 접두사를 찾는 방법을 Sn까지 거듭해서 반복하는것이다.
-> LCP(S1, S2, ..., Sn) = LCP(LCP(LCP(S1, S2), S3), ... Sn)
public Sting longestCommonPrefix(String[] strs) {
if(str.length == 0) {
return "";
}
String prefix = strs[0];
for(int i = 1; i <str.length; i++) {
while(str[i].indexOf(prefix) != 0) {
// 접두사문자열을 하나씩 줄여나가며 공통 접두사를 찾아나간다.
prefix = prefix.substring(0, prefix.length() - 1);
if(prefix.isEmpty()) {
return "";
}
}
}
return prefix;
}
복잡도 분석 (Complexity Analysis)
-
시간 복잡도 (Time Complexity)
O(s), S는 모든 문자열에 있는 모든 문자들의 합이다.
최악의 경우는 n개의 문자열들이 모두 같은 경우이다.
이 알고리즘은 문자열 S1과 다른 문자열 S2부터 Sn까지를 비교한다.
그리고 입력배열에서 모든 문자들의 합계인 S만큼 비교하게 되는것이다 -
공간 복잡도 (Space Complexity)
O(1)
접근법 #2. Vertical Scanning
기준이 되는 문자열과 나머지 문자열을 수직방향으로 탐색해나가는 방법이다.
여기서 기준문자열은 문자열배열의 첫번째 문자열이 된다.
기준 문자열의 문자를 하나씩 순회할때마다 (순회당시 인덱스 값이 i라고 하면)
배열의 나머지 문자열들의 i번째 문자가 기준 문자열의 문자값과 일치하는지를 체크해준다.
public String longestCommonPrefix(String[] strs) {
if (str == null || str.length == 0) {
return "";
}
for (int i = 0; i < strs[0].length; i++) {
char c = strs[0].charAt(i);
for(int j = 1; j <strs.length; j++) {
if(i == str[j].length || str[j].charAt(i) != c) {
return sts[0].substring(0, i);
}
}
}
}
복잡도 분석 (Complexity Analysis)
-
시간 복잡도 (Time Complexity)
O(s), S는 모든 문자열에 있는 모든 문자들의 합이다.
최악의 경우는 길이가 m개인 문자열이 n개있는 경우이다.
그러면 이 알고리즘은 S = m * n만큼의 비교를 수행하게 된다.
비록 최악의 경우가 접근법1과 비슷해보이지만, 최고의 경우는 기껏해야 n * 최소길이의 비교가 된다.
여기서 최소 길이는 문자열 배열에서 가장 짧은 길이를 가진 문자열의 길이가 된다. -
공간 복잡도 (Space Complexity)
O(1)
접근법 #3. Divide and Conquer
문자열 Si부터 Sj까지의 가장 긴 공통의 접두사를 구하는 식은 LCP(Si, .. , Sj)라고 하자.
그리고 큰 하나의 문제를 LCP(Si, …, Smid)와 LCP(Smid+1, …, Sj)로 2개의 부분문제로 분할한다.
여기서 mid값은 i와 j의 중간값(i+j/2)이 된다.
lcpLeft와 lcpRight 솔루션을 사용하여 문제 LCP(Si, …, Sj)의 해를 구한다.
해를 구하기 위해 우리는 lcpLeft에 있는 문자와 lcpRight에 있는 문자 하나하나를 비교하면서 일치하지 않는 문자가 있는 부분을 찾아낸다.
public String longestCommonPrefix(String[] strs) {
if(strs = null strss.lenth == 0) {
return "";
}
return longestCommonPrefix(strs, 0, srs.length-1);
}
public String longestCommonPrefix(String[] strs, int l, int r) {
if(l == r) {
return strs[l];
} else {
int mid = (l + r) / 2;
String lcpLeft = longestCommonPrefix(strs, l, mid);
String lcpRight = longestCommonPrefix(str, mid+1, r);
return commonPrefix(lcpLeft, lcpRight);
}
}
public String commonPrefix(String left, String right) {
int min = Math.min(left.length(), right.length());
for(int i = 0; i <min; i++) {
if(left.charAt(i) != right.charAt(i)) {
return left.substring(0, i);
}
}
return left.substring(0, min);
}
Subscribe via RSS
